Was sind Multilevel Modelle?

Um Multilevel-Modelle zu erklären, holen wir in diesem Skript anhand eines Beispiels etwas aus. Stellen wir uns einmal folgende Situation vor: Sie haben den Auftrag, im Rahmen eines pädagogisch-psychologischen Projektes die Effektivität von Achtsamkeitsübungen in der Praxis zu untersuchen. Die Theorie: Durch eine kurze Achtsamkeitsübung am Beginn einer Schulstunde sinkt die Unruhe in der Klasse, was zu einem besseren Lernklima führt. Bevor Sie enorme Ressourcen aufwenden, um die Frage in einem groß angelegten Feld-Experiment zu untersuchen, werten Sie vorhandene Daten aus.

Die Story: Schulen in Mittelerde

Und Sie haben Glück: Es gibt einen sehr ergiebigen Datensatz über acht Schulen in Mittelerde, den sie nutzen können. Einige Klassenlehrer, sowohl in Gondor, als auch in Rohan, haben sich von den Elben überzeugen lassen, routinemäßig zu Beginn jeder Unterrichtsstunde eine Achtsamkeitsmeditation durchzuführen. Im Datensatz finden Sie Informationen zur Lesefertigkeit der Schüler:innen am Ende der 9. Klasse und Informationen über die Schule. Die Lesefertigkeit verwenden wir hier als abhängige Variable, da wir ein besseres Lernklima dadurch definieren, dass die Schüler:innen bessere Leistung erbringen. Hier ein Blick in die Daten:

pupil_id realm school mindfulness class reading_skill
592 gondor (G) Arwen-Abendstern-Schule FALSE b 36.6
373 gondor (G) Gandalf-Gymnasium FALSE c 32.6
209 rohan (R) Schildmaid-Eowyn-Schule TRUE b 28.6
11 rohan (R) König-Theoden-Gesamtschule TRUE a 28.9
212 rohan (R) Schildmaid-Eowyn-Schule TRUE b 33.4

Weitere Eckdaten:

Die Analyse

Wir fangen zur Einordnung mit einer einfachen Regression an und gehen noch einmal die Bestandteile eines einfachen Regressionsmodells durch. Wir rechnen folgende Regression:

\[ y_i = \hat{\beta}_0 + \hat{\beta}_1 \cdot x_i + \hat{\epsilon}_i \]

Dabei ist

  • \(y_i\) die Lesefertigkeit von Schüler:in \(i\),

  • \(x_i\) ein Indikator dasfür, ob Schüler:in \(i\) in einer Klasse ist, in der Achtsamkeitsübungen durchgeführt werden (0 = Nein, 1 = Ja),

  • und \(\hat{\beta}_1\) der geschätzte mittlere Unterschied in der Lesefertigkeit zwischen Schüler:innen, die Achtsamkeitsübungen erfahren und solchen, die keine Achtsamkeitsübungen erfahren.

  • \(\hat{\epsilon}_i\) der geschätzte Fehler, also der Unterschied zwischen unserem geschätzten Wert der Lesefertigkeit auf Grundlage von \(x_i\) und der tatsächlichen, gemessenen Lesefertigkeit.

Hier der R-Output zur Regression:

## 
## Call:
## lm(formula = reading_skill ~ mindfulness, data = data)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -23.5486  -5.2078   0.5343   5.3678  19.8172 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)      31.5486     0.4344   72.62  < 2e-16 ***
## mindfulnessTRUE  -2.2659     0.6192   -3.66 0.000273 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 7.88 on 646 degrees of freedom
## Multiple R-squared:  0.02031,    Adjusted R-squared:  0.01879 
## F-statistic: 13.39 on 1 and 646 DF,  p-value: 0.0002733

Wir sehen, dass \(\hat{\beta}_1\) auf ca. -2.3 geschätzt wird, und dass dieses Ergebnis unter der Nullhypothese \(\hat{\beta}_1 = 0\) nur mit einer Wahrscheinlichkeit von p < .001 auftreten würde. Unsere Schätzung aufgrund dieser Analyse lautet also, dass Achtsamkeitsübungen mit einer um ca. 2.3 Punkte schlechteren Lesefertigkeit zusammenhängen. Ein Plot scheint diesen Eindruck zu bestätigen:

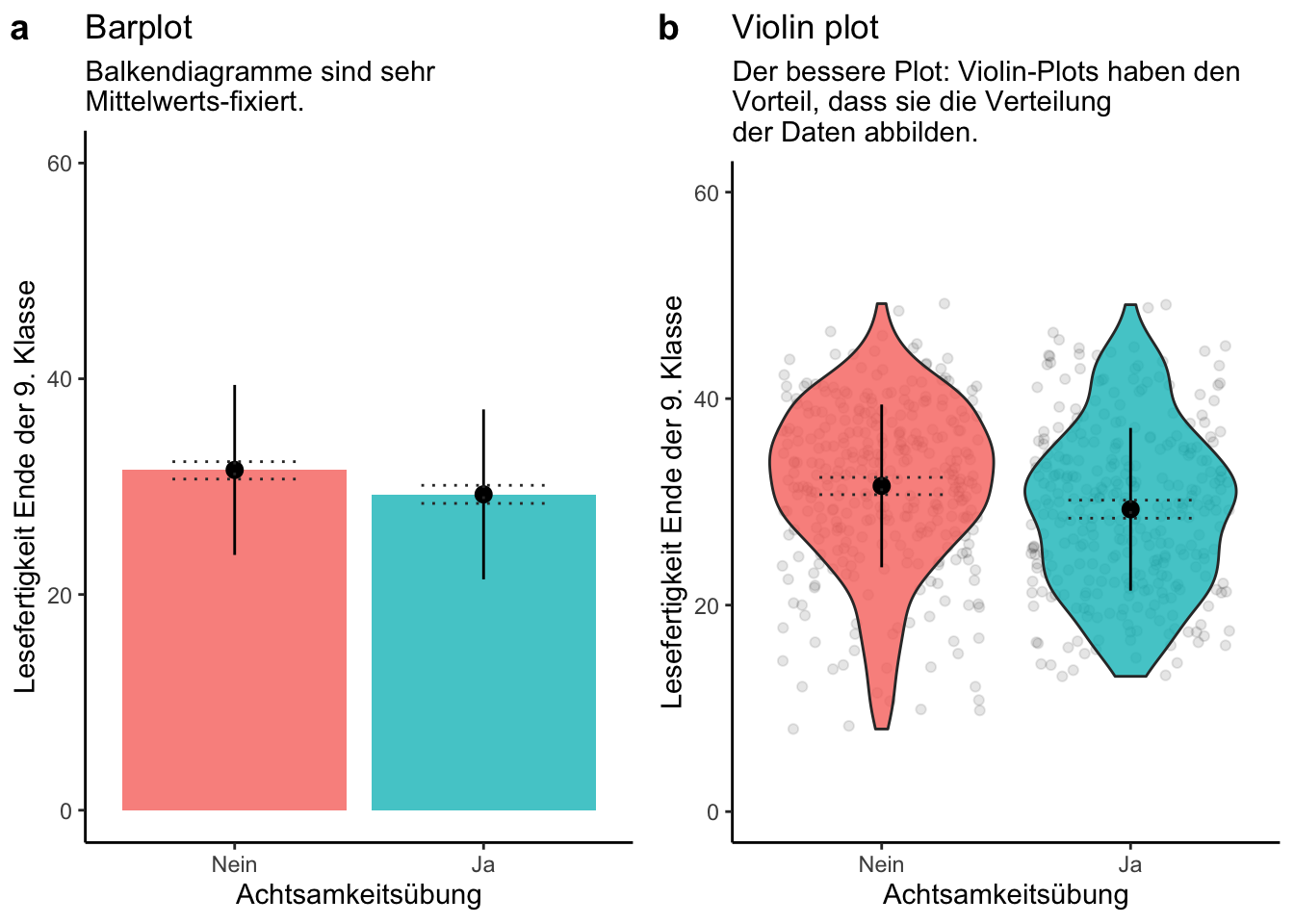
**Abbildung**: Mittlere Lesefertigkeiten in Schulklassen, in denen Achtsamkeitsübungen durchgeführt oder nicht durchgeführt werden. Die Plots a) und b) zeigen die gleichen Daten, einmal als Balkendiagramm und einmal als Violin-Plot mit Rohdaten im Hintergrund (jeder Datenpunkt bezieht sich auf eine:n Schüler:in). Fehlerbalken zeigen plus/minus eine Standardabweichung in der Lesefertigkeit um den Mittelwert. Gepunktete Linien zeigen 95%-Konfidenzintervalle für die Mittelwerte.

Abbildung: Mittlere Lesefertigkeiten in Schulklassen, in denen Achtsamkeitsübungen durchgeführt oder nicht durchgeführt werden. Die Plots a) und b) zeigen die gleichen Daten, einmal als Balkendiagramm und einmal als Violin-Plot mit Rohdaten im Hintergrund (jeder Datenpunkt bezieht sich auf eine:n Schüler:in). Fehlerbalken zeigen plus/minus eine Standardabweichung in der Lesefertigkeit um den Mittelwert. Gepunktete Linien zeigen 95%-Konfidenzintervalle für die Mittelwerte.

Nebenbei bemerkt: Unsere Darstellung mit Standardabweichungen als “Pointrange”/Fehlerbalken und Konfidenzintervallen als gestrichelten Linien ist etwas ungewöhnlich. Häufig findet man Darstellungen der Konfidenzintervalle oder Standardfehler als Fehlerbalken. Wir wählen die hier gezeigte Darstellung, da sie unserer Ansicht nach einen vollständigeren Eindruck der Daten vermittelt: Das Konfidenzintervall gibt einen Eindruck über die Schätzunsicherheit (es ersetzt damit eine Darstellung des Standardfehlers und ist besser verständlich) und die Standardabweichung gibt einen Eindruck über die Varianz der zugrundeliegenden Daten. Mehr dazu hier: Uncertainty and variation as distinct concepts

Der Haken

Der Haken ist: Wir haben zwar eine große Stichprobe und für sich genommen tolle Daten, doch es handelt sich hier um kein experimentelles Design. Das heißt genauer:

  • Wir vergleichen zwar gewissermaßen eine Kontroll- und eine Experimentalgruppe miteinander, aber diese Gruppen wurden nicht zufällig eingeteilt. Wir haben stattdessen Daten genommen, die uns ohnehin vorlagen. Damit besteht ein großes Risiko für Konfundierung. (Anmerkung: Das trifft auf unseren Beispiel-Datensatz zu, muss aber nicht für alle Multilevel-Datensätze gelten.)

  • In unserem Datensatz haben wir zusätzlichen Grund, Verzerrungen zu vermuten, denn unsere Beobachtungen sind nicht unabhängig voneinander: Unser Datensatz lässt sich systematisch in zusammengehörige Untergruppen einteilen (siehe Abbildung unten). Schüler:innen aus der gleichen Klasse oder Schule sind sich vermutlich untereinander ähnlicher, als Schüler:innen aus verschiedenen Schulen oder gar verschiedenen Reichen. Die Unabhängigkeit aller Datenpunkte ist allerdings eine zentrale Annahme für die Gültigkeit unserer statistischen Analyse.

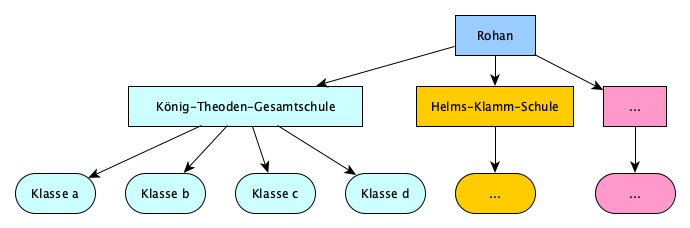
Abbildung: Systematische Gruppen in unserem Datensatz, hier innerhalb Rohans dargestellt.

Warum ist der Haken wichtig?

Das wird am besten deutlich, wenn wir eine ausgefeiltere Analyse anwenden, mit der wir die Beziehungen innerhalb unseres Datensatzes explizit berücksichtigen. In einer Regressionsgleichung, in der wir Korrelationen innerhalb von Schulen berücksichtigen wollen, sieht das ungefähr so aus:

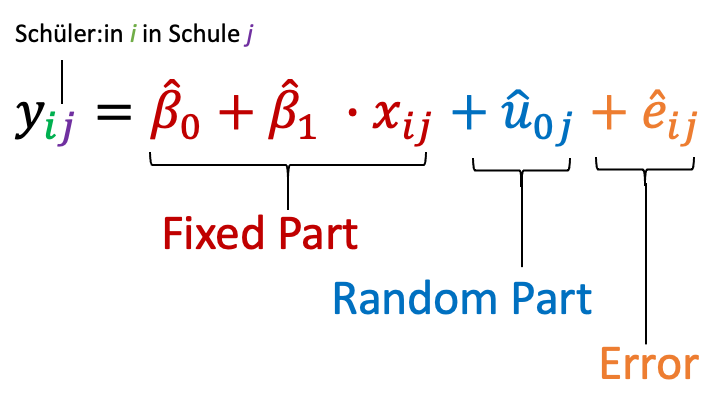
Die Formel zeigt eine Multilevel-Regression. Dabei ist für uns insbesondere der fixed effect \(\hat{\beta}_1\) interessant; das ist praktisch die gleiche Größe wie in der normalen Regression. Der Unterschied ist, dass wir durch den random effect \(\hat{u}\_{0j}\) die Unterschiede zwischen den Schulen explizit berücksichtigen und aus unserer Schätzung für \(\hat{\beta}_1\) “herausrechnen” können. Schauen wir uns zu dieser Analyse nun einen Plot an, so sehen wir: In jeder einzelnen Schule für sich genommen sind die Achtsamkeitsübungen tatsächlich mit besseren Leseleistungen assoziiert.

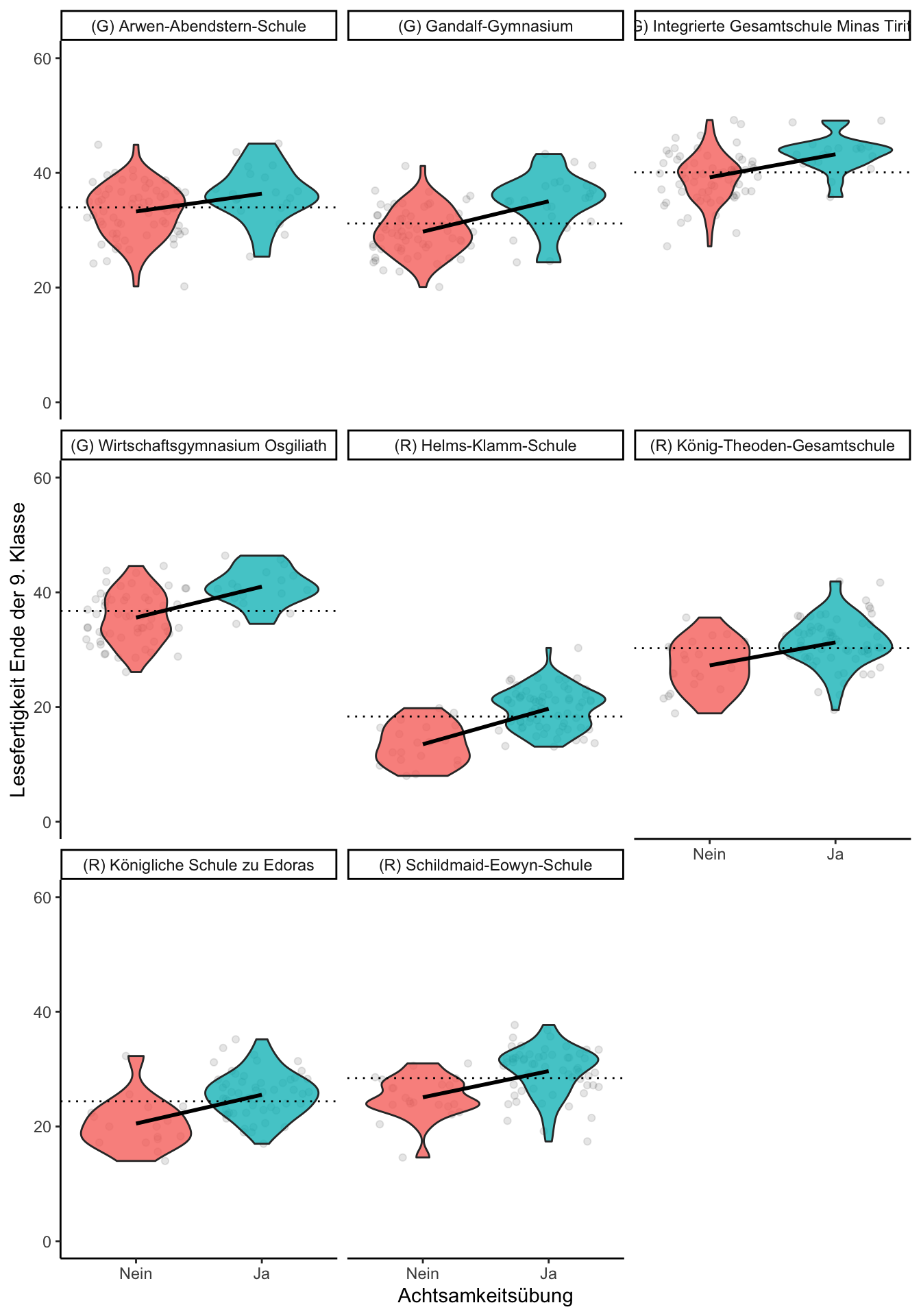
**Abbildung**: Violin-Plot der Lesefertigkeit in Klassen mit und ohne Achtsamkeitsübungen. Gepunktete Linie zeigt den Schul-Mittelwert.

Abbildung: Violin-Plot der Lesefertigkeit in Klassen mit und ohne Achtsamkeitsübungen. Gepunktete Linie zeigt den Schul-Mittelwert.

Die Analyse per Multilevel-Regression bestätigt den Eindruck aus den Plots: Wir bekommen eine Schätzung von \(\hat{\beta}_1\) = 4.7, d.h. im Mittel sind Achtsamkeitsübungen mit einer um etwa 4.7 Punkte besseren Lesefähigkeit assoziiert.

Wir zeigen an dieser Stelle bewusst nicht die Details der Spezifikation. Ziel dieses Skriptes ist, auf grober Ebene das Konzept von Multilevel-Analysen zu verdeutlichen. Die praktische Durchführung wird bspw. in Field (2012) besprochen.

## Linear mixed-effects model fit by REML
##  Data: data 
##        AIC      BIC    logLik
##   3725.124 3743.007 -1858.562
## 
## Random effects:
##  Formula: ~1 | school
##         (Intercept) Residual
## StdDev:    8.001673 4.130592
## 
## Fixed effects: reading_skill ~ mindfulness 
##                     Value Std.Error  DF   t-value p-value
## (Intercept)     28.121496 2.8400089 639  9.901904       0
## mindfulnessTRUE  4.661775 0.3823333 639 12.192961       0
##  Correlation: 
##                 (Intr)
## mindfulnessTRUE -0.067
## 
## Standardized Within-Group Residuals:
##         Min          Q1         Med          Q3         Max 
## -3.07419705 -0.66535567  0.05011898  0.65108909  2.90557507 
## 
## Number of Observations: 648
## Number of Groups: 8

Jetzt noch einmal eingeordnet in unsere Perspektiven:

Wissenschaftliche Perspektive | Die wissenschaftliche Perspektive stellt den Erkenntnisgewinn in den Mittelpunkt: Stimmt unsere Theorie? Wie groß und wie zuverlässig ist der Effekt? Welche Faktoren beeinflussen das Ergebnis?

  • Wenn wir Daten mit hierarchischen Strukturen (z.B. Schüler in Klassen in Schulen in Ländern, …) analysieren, dann wird ggf. die Annahme unabhängiger Beobachtungen verletzt. Diese Annahme ist wichtig für klassische statistischer Verfahren wie t-Test, ANOVA und Regression (t-Test und ANOVA sind nur andere Darstellungen von Regressionen).

  • Wenn die Unabhängigkeitsannahme verletzt wird, kann es sein, dass die Schlussfolgerungen statistischer Analysen falsch sind. Genau genommen ist in diesem Fall (d.h., wenn tatsächlich die Unabhängigkeitsannahme verletzt ist) eine solche Analyse unbrauchbar, um Hypothesen zu testen.

Praktiker-Perspektive | Die praktische Perspektive stellt die Nützlichkeit einer aus der Forschung abgeleiteten Intervention in den Mittelpunkt: Sollten wir die Intervention einsetzen?

  • Wenn die Datenanalyse einer empirischen Studie nicht geeignet ist, die vorgestellte Theorie oder Hypothese angemessen zu testen, dann bietet sie keine gute Grundlage für praktische Entscheidungen.

  • Solche Analysen sollten deshalb nicht als einzige Evidenz zur Bedrüngung von praktischen Entscheidungen verwendet werden. Vielmehr sollten sich Praktiker als Risikomanager:innen verstehen und die theoretische Plausibilität und empirische Evidenz ganzheitlich betrachten. Auf dieser Basis können sie verschiedene Szenarien abwägen und eine bestmöglich fundierte Entscheidung treffen.

  • Dahingehend treffen die gleichen, detaillierteren Überlegungen zu, die wir in unserem Artikel zu Konfundierung (siehe “Warum ist der Haken wichtig?”) geschildert haben.

Ein paar Hinweise zu Multilevel-Modellen

  • Hier haben wir als Beispiel nicht-experimentelle Querschnittsdaten zur Veranschaulichung eines Multilevel-Modells genommen. Je nach Versuchsdesign kann es aber auch in randomisierten Experimenten durchaus sein, dass hierarchische Daten entstehen, bspw. wenn Versuchspersonen in Untergruppen eingeteilt werden. Das sollte bei der Analyse berücksichtigt werden!

  • Ein häufiger Anwendungsfall für Multilevel-Modelle sind auch Messwiederholungsdaten. Dabei sind die einzelnen Messzeitpunkt in Versuchspersonen genestet.

  • Es gibt keine objektive, immer zutreffende Regel dafür, um zu entscheiden, welche Effekt als fixed und welche als random Effekte modelliert werden. Hier müssen theoriegeleitete Entscheidungen getroffen werden. Die Leitfrage, um diese Entscheidung zu treffen ist: „Welcher Effekt ist von wissenschaftlichem Interesse für mich?" Das ist tendenziell ein fixed Effekt. Auch die umgekehrte Frage ist hilfreich: „Welcher Effekt hat möglicherweise einen verzerrenden Einfluss, den ich ‘herausrechnen’ möchte?" Das ist tendenziell ein random Effekt.

  • Es kann durchaus sein, dass Daten eine hierarchische Struktur ähnlich der hier vorgestellten aufweisen, ohne dass eine Modellierung in einem Multilevel-Modell notwendig ist. Dafür kann z.B. die Intraclass Correlation (ICC) berechnet werden; eine Korrelation, die angibt, wie ähnlich sich Beobachtungen innerhalb einer Gruppe sind. Eine hohe ICC deutet darauf hin, dass eine Multilevel-Analyse sinnvoll ist. Für Details verweisen wir auf Field (2012).

Begriffliche Verwirrungen bei Multilevel-Modellen

  • Daten mit Hierarchischen Strukturen werden oft auch als genestete Daten bezeichnet. Im hier behandelten Beispiel würde man sagen, dass Beobachtungen von Schüler:innen in Schulen und Schulen in Ländern genestet sind.

  • Für Multilevel-Modelle existieren eine Reihe von Bezeichnungen, die häufig praktisch synonym verwendet werden. Beispiele sind:

    • Linear mixed effects regression. Das “mixed” soll hier verdeutlichen, dass sowohl “fixed”, als auch “random” Effekte im Modell aufgenommen werden.

    • Hierarchical linear models. Achtung: Hier besteht Verwechslungsgefahr zum Schrittweisen vorgehen bei Regressionsanalysen (Modellvergleichende Tests zur Identifikation des am besten passenden Modells). Dieses Schrittweise Vorgehen wird gerade unter Psycholog:innen auch häufig “Hierarchical Regression” genannt, beinhaltet aber nicht notwendigerweise Multilevel Regressionen.

    • Multilevel models.