Nullhypothesen-Signifikanztesten
Johannes Brachem & Christian Treffenstädt
Es gibt verschiedene Paradigmen, in denen wir Statistik betreiben können. Das in der Psychologie und vielen anderen Sozialwissenschaften am weitesten verbreitete ist das Nullhypothesen-Signifikanztesten (NHST, auch frequentistische Statistik genannt, genau genommen bezeichnet der Begriff der frequentistischen Statistik aber ein noch etwas weiteres Feld als NHST).
Dieses Paradigma wird in den vergangenen Jahren zunehmend kontrovers diskutiert - und mit der Bayesschen Statistik gibt es eine starke alternative Herangehensweise. Nichtsdestotrotz ist das NHST aktuell der häufigste Ansatz. Ohne NHST zu verstehen können wir weder psychologische Forschung verstehen, noch eine sinnvolle Einschätzung der Debatte um NHST vs. Bayes entwickeln. Deshalb gehen wir in diesem Skript ein wenig näher auf die Logik des NHST ein. Das Skript steht in engem Zusammenhang zu unseren vorherigen Ausführungen zu Signifikanz und Effektsärke und zur Interpretation von Befundmustern.

Abbildung 1. XKCD-Comic zum Nullhypothesentesten.
Die Logik des Testens von Nullhypothesen
Wenn wir eine Vermutung (Hypothese, H1) über die Welt haben, dann sammeln wir Daten, um diese Vermutung zu überprüfen. Im Rahmen des NHST findet diese Überprüfung indirekt statt, indem wir unserer Vermutung die sogenannte Nullhypothese (H0) gegenüberstellen. Wenn wir dann also unsere Daten sammeln und auswerten, schauen wir nach bestimmten Mustern (bspw., dass ein Mittelwert in einer Gruppe größer ist als in einer anderen). Wir berechnen dann, wie wahrscheinlich es wäre, dieses Muster zu finden, wenn die Nullhypothese stimmen würde. Das ist der p-Wert. Im Vorhinein definieren wir, wie unwahrscheinlich ein Muster unter der Nullhypothese sein muss, damit wir sie verwerfen. Das ist das Alpha-Niveau \(\alpha\), das per sozialer Norm oft auf 5 %, bzw. \(\alpha = 0.05\) gesetzt wird. Wenn die Wahrscheinlichkeit unserer Daten bei Annahme der Nullhypothese unter dem Alpha-Niveau liegt, verwerfen wir also die Nullhypothese und werten unsere Daten als Evidenz für die H1, auch Alternativhypothese genannt.
Die Argumentation ist in diesem Fall die Folgende:
“Wenn kein Effekt vorliegen würde (H0 stimmt), dann wäre es sehr unwahrscheinlich, dass sich ein Muster wie in unseren Ergebnissen zeigen würde. Deshalb ist es nicht vernünftig, anzunehmen, dass kein Effekt vorliegt. Wir verwerfen also die H0 und nehmen stattdessen an, dass ein Effekt vorliegt, der zumindest irgendwie verschieden von 0 ist.”
Schlussfolgerungen über die H1
Wir können dabei in Bezug auf die H1 vier Arten von Schlussfolgerungen ziehen, die in Tabelle 1 aufgezeigt werden: Richtig positiv, falsch positiv, Richtig negativ und falsch negativ. Durch das Alpha-Niveau können wir kontrollieren, wie häufig wir falsch positive Entscheidungen treffen, im üblichen Fall von \(\alpha = 0.05\) werten wir mit NHST-Tests also in 5 % oder einem von 20 Fällen eine Studie als Evidenz für eine Hypothese, die nicht stimmt.
| Wirklichkeit | Test-Entscheidung | Schlussfolgerung | Bezeichnung | Wahrscheinlichkeit |
|---|---|---|---|---|
| H0 stimmt | H0 beibehalten | Richtig negativ | Spezifität | \(1-\alpha\) |
| H0 stimmt | H0 verwerfen | Falsch positiv | Typ 1 Fehler | \(\alpha\) |
| H1 stimmt | H0 verwerfen | Richtig positiv | Power/Teststärke | \(1-\beta\) |
| H1 stimmt | H0 beibehalten | Falsch negativ | Typ 2 Fehler | \(\beta\) |
Neben dem Alpha-Niveau \(\alpha\) ist auch \(\beta\), die Wahrscheinlichkeit, dass wir einen tatsächlich vorhandenen Effekt nicht entdecken, eine wichtige Größe, wobei meistens über den umgekehrten Fall \(1 - \beta\) gesprochen wird, also die Power: die Wahrscheinlichkeit, einen tatsächlich vorhandenen Effekt zu entdecken. Während \(\alpha\) in der Regel von den Forscher:innen einfach festgelegt wird, ist die Power von mehreren Faktoren abhängig: Von \(\alpha\), von der betrachteten Effektstärke, und von der Stichprobengröße (siehe “Effektstärke und Signifikanz hängen zusammen”).
In der Praxis müssen wir wegen des Zusammenhangs von Power und Alpha-Niveau häufig zwischen beiden abwägen; vor allem dann, wenn wir keine unendlich großen Stichproben zur Verfügung haben. Wir können ein größeres Risiko für falsch-positive Befunde eingehen und dadurch unser Risiko für falsch-negative Befunde senken, indem wir ein höheren Alpha-Niveau ansetzen, bspw. \(\alpha = 0.20\). Wir können umgekehrt unser Risiko für falsch-positive Befunde verringern und ein höheres Risiko für falsch-negative Befunde eingehen, indem wir das Alpha-Niveau verringern, bspw. auf \(\alpha = 0.01\). Wenn wir allerdings unsere Stichprobengröße erhöhen können, dann können wir die Power steigern, ohne dafür mit Alpha-Niveau zu “bezahlen”.
Die unten stehenden Boxen zeigen mögliche qualitative Überlegungen zur Abwägung von Alpha-Niveau und Power auf. Dabei nennen wir keine konkreten Zahlen, denn der Punkt dieser Beispiele ist es, deutlich zu machen, dass qualitative Risikoabschätzungen und Werturteile eine wesentliche Rolle bei der Abwägung von Alpha-Niveau und Power spielen.
Beispiel 1: Die Wirkung eines Medikaments
Nehmen wir als Beispiel eine Studie, in der die Wirkung des (fiktiven) Krebs-Medikaments Cancipex untersucht werden soll. Wir fragen uns, welches Alpha-Niveau wir ansetzen sollten. Wir haben nur eine feste, begrenzte Stichprobe zur Verfügung, deshalb müssen wir Überlegungen zu sinnvollen Effektstärken anstellen und mit der Festsetzung des Alpha-Niveaus eine Balance aus Power und falsch-positiv-Rate finden. Dazu stellen wir folgende Überlegungen an:
Wenn wir eine falsch-positives Schlussfolgerung ziehen, gehen wir das Risiko ein, dass Patient:innen mit unwirksamen Medikamenten behandelt werden. Das bedeutet gleichzeitig, dass sie in dem Zeitraum, in dem sie Cancipex erhalten, andere Medikamente nicht erhalten. Bei Krebs kann das den Unterschied zwischen Leben und Tod ausmachen. Ein falsch-positives Ergebnis wäre furchtbar, deshalb sollten wir nicht leichtfertig das Alpha-Niveau erhöhen.
Wenn wir eine falsch-negative Schlussfolgerung ziehen, gehen wir das Risiko ein, dass Patient:innen ein wirksames Mittel nicht erhalten. Das ist vor allem dann schlimm, wenn Cancipex wirksamer als herkömmliche Mittel ist. In unsere Überlegungen zur Power können wir die Effektstärke der besten Alternative zu Cancipex einbeziehen: Wenn die Wirkung der Alternative einer großen Effektstärke entspricht, dann reicht es für uns aus, mit einer hohen Wahrscheinlichkeit eine stärkere Wirksamkeit von Cancipex zu entdecken.
In diesem Beispiel ist es unserer Einschätzung nach sinnvoll, ein besonderes Augenmerk auf die Minimierung der falsch-positiv-Rate zu legen. Wenn wir also die Stichprobengröße nicht mehr erhöhen können, würde das bedeuten, einem kleineren \(\alpha\) tendenziell mehr Bedeutung zuzugestehen, als einer größeren Power. Das Alpha-Niveau könnte bspw. auf \(\alpha = 0.01\) festgesetzt werden, so dass nur in einem von 100 Fällen (statt in einem von 20 Fällen beim Standard-Niveau von 0.05) eine falsch-positive Schlussfolgerung gezogen wird. In der Praxis sollte im Vorhinein beachtet werden, was die kleinste interessante Effektsärke wäre, um auf dieser Basis zu einer informierten Abwägung von Alpha-Niveau und Power zu kommen.
Beispiel 2: Die Umweltschädlichkeit eines Unkrautvernichtungsmittels
Nehmen wir als zweites Beispiel eine Studie, in der die Umweltschädlichkeit eines Unkrautvernichtungsmittels untersucht werden soll. Auch hier fragen wir uns, welches Alpha-Niveau wir ansetzen sollten und haben nur eine feste, begrenzte Menge von Daten zur Verfügung. Wir stellen folgende Überlegungen an:
Wenn wir eine falsch-positive Schlussfolgerung ziehen (d.h. wir folgern fälschlicherweise, dass das Mittel umweltschädlich ist), gehen wir das Risiko ein, dass ein umweltverträgliches Mittel verboten wird und damit der Landwirtschaft nicht zur Verfügung steht. Das könnte negative wirtschaftliche Konsequenzen haben. Andererseits sind eine Menge Alternativen verfügbar, so dass wir keinen allzu großen Schaden von einem falsch-positiven Ergebnis erwarten würden. Wir sind also in Bezug auf das Alpha-Niveau hier flexibler als beim Krebs-Medikament.
Wir wir eine falsch-negative Schlussfolgerung ziehen, gehen wir das Risiko ein, dass ein umweltschädliches Mittel zugelassen wird. Der Einsatz eines solchen Mittels kann ungeahnte Konsequenzen für die komplexen Ökosysteme haben, von denen wir umgeben sind. Der Einsatz solcher Mittel spielt möglicherweise eine Rolle dabei, dass die Biomasse an Insekten in Deutschland seit 1989 um erschreckende 78 % zurückgegangen ist (Quelle). Das ist also ein enormes Risiko, bei dem sich Vorsicht lohnt.
In diesem Beispiel ist es unserer Einschätzung nach sinnvoll, die Minimierung der falsch-negativ Rate besonders zu gewichten. Wenn wir also die Stichprobengröße nicht mehr erhöhen können, würde das bedeuten, ggf. ein höheres Alpha von bspw. \(\alpha = 0.20\) zu wählen. Wir würden so zwar in einem von 5 Fällen ein unschädliches Mittel nicht zulassen, könnten aber die Gefahr minimieren, dass wir ein schädliches Mittel nicht als schädlich erkennen. In der Praxis müssten wir zunächst analysieren, wie groß die kleinste für uns interessante Effektstärke wäre, um auf dieser Basis zu einer informierten Abwägung von Alpha-Niveau und Power zu kommen.
Die in diesem Skript genannten Alpha-Niveaus sind soziale Konventionen:
- \(\alpha = 0.05\) ist das “Standard” Alpha Niveau
- \(\alpha = 0.20\) ist ein hohes Alpha-Niveau, mit dem die Nullhypothese bei konstanter Stichprobengröße und Effektstärke stärker getestet werden kann. Es ist auf Minimierung der falsch-negativ-Rate in Bezug auf die H1 ausgelegt.
- \(\alpha = 0.01\) ist ein niedrigeres, also strengeres, Alpha-Niveau, mit dem die falsch-positiv-Rate verringert werden kann.
Man sollte diese sozialen Konventionen kennen, sich von ihnen aber nicht blenden lassen. Wichtig ist vor allem, dass Forscher:innen vor der Datenerhebung sinnvolle Alpha-Niveaus festlegen und eine sinnvolle Stichprobenplanung für angemessene Power unternehmen. In der Forschung gibt es intensive (und sehr lehrreiche) Debatten um die Festzsetzung von Alpha-Niveaus. Drei wichtige Beiträge, mit denen Interessierte Einblick in die Debatte nehmen können, sind unten in der Literaturliste zu finden.
Schlussfolgerungen über die H0
In unseren bisherigen Ausführungen haben wir dargelegt, wie wir auf Basis der H0 indirekt Schlussfolgerungen über die Plausibilität der H1 zu ziehen versuchen. Können wir gleichzeitig auch Schlussfolgerungen über die H0 ziehen? Immerhin wäre es sehr interessant, wenn wir schlüssig argumentieren könnten, dass die H0 stimmt. Leider ist die Sache nicht so einfach. Nehmen wir als Ausgangspunkt für diesen Abschnitt einen prägnanten Merksatz:
“Absence of evidence is not evidence of absence”
Dieser Merksatz enthält eine wichtige Einsicht über das Testen der Nullhypothese: Wenn wir die Nullhypothese nicht verwerfen können, also keine Evidenz für die H1 finden, dann bedeutet das nicht automatisch, dass wir Evidenz für die H0 vorliegen haben. Ein solches Ergebnis sagt lediglich aus, dass die vorliegenden Daten unter der Annahme der Nullhypothese nicht besonders unwahrscheinlich wären. Das reicht als Evidenz für die H0 nicht aus, denn es ist häufig der Fall, dass die Power des Tests schlicht nicht ausreichte, um einen Effekt mit guter Wahrscheinlichkeit finden zu können. Deshalb nennen wir einen Befund, bei dem wir die Nullhypothese nicht verwerfen können, einen Nullbefund, oder einfach nicht aussagekräftig.
Trotzdem sollten wir diesen Merksatz nicht als absolute Wahrheit überhöhen, denn es gibt durchaus wertvolle Informationen, die in einem Nullbefund stecken können. Das wird klarer, wenn wir uns die Konfidenzintervalle der Effektschätzung ansehen. Die 95 %-Konfidenzintervalle zeigen uns einen Bereich um die Punktschätzung eines Effekts, der mit 95 %iger Wahrscheinlichkeit den echten Effekt beinhaltet. Wenn das Konfidenzintervall den Wert “0” nicht einschließt, ist das gleichbedeutend mit einem signifikanten Testergebnis (es ist sogar rechnerisch genau das selbe!). Wenn das Konfidenzintervall nun aber den Wert 0 einschließt, dann können wir aus dem Intervall ablesen, in welchem Bereich wahrscheinliche Werte liegen. So können wir eine zusätzlich Aussage darüber treffen, ob der Effekt signifikant kleiner als ein Referenzwert ist. Dieser Referenzwert kann, bzw. sollte die kleinste Effektstärke sein, die für uns von Bedeutung ist. In diesem Fall können wir davon reden, dass ein Effekt praktisch äquivalent zu 0 ist. Abbildung 2 zeigt vier Beispielszenarien für den Fall eines arbiträren Referenzwerts von 0.5.
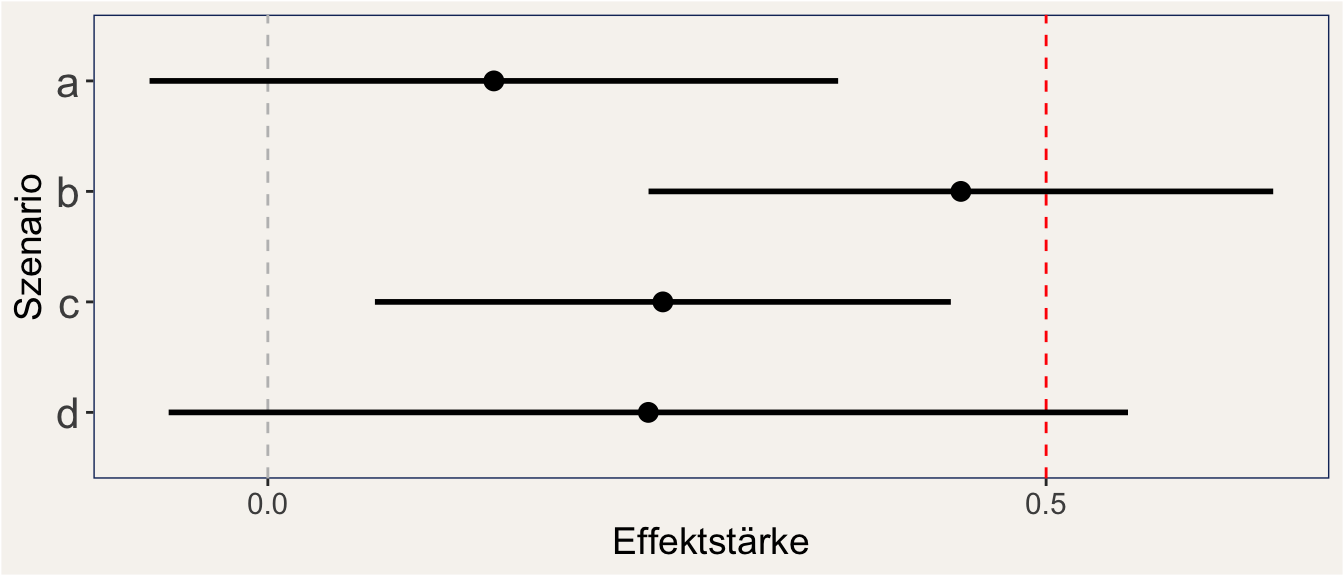
Abbildung 2. Beispielszenarien bei der Untersuchung von Konfidenzintervallen. Horizontale Linien zeigen 95 % Konfidenzintervalle. Die Darstellung ist entlehnt von Lakens (2017).
Gehen wir die vier Szenarien Schritt für Schritt durch:
- Szenario a: Der Effekt ist nicht signifikant verschieden von 0, da das Konfidenzintervall 0 einschließt. Zusätzlich ist der Effekt auch praktisch äquivalent zu 0, da das Konfidenzintervall den Referenzwert 0.5 nicht einschließt.
- Szenario b: Der Effekt ist signifikant verschieden von 0, da das Konfidenzintervall 0 nicht einschließt. Zusätzlich ist der Effekt auch praktisch nicht äquivalent zu 0, da das Konfidenzintervall den Referenzwert 0.5 einschließt.
- Szenario c: Der Effekt ist signifikant verschieden von 0, da das Konfidenzintervall 0 nicht einschließt. Er ist aber praktisch äquivalent zu 0, da das Konfidenzintervall den Referenzwert 0.5 ebenfalls nicht einschließt. Das ist der Fall eines signifikanten Effekts, der so klein ist, dass er uns praktisch nicht interessiert (siehe Effektstärke und Signifikanz).
- Szenario d: Der Effekt ist nicht signifikant verschieden von 0, da das Konfidenzintervall 0 einschließt. Er ist aber auch nicht praktisch äquivalent zu 0, da das Konfidenzintervall den Referenzwert 0.5 ebenfalls einschließt.
Diese Überlegungen liegen den sogenannten Äquivalenztests zugrunde. Sie sind in der Psychologie noch nicht weit verbreitet, aber Lakens bietet eine gute Erklärung (Lakens, 2017) und ein Tutorial (Lakens, Scheel & Isager, 2018).
Neben den Konfidenzintervallen kann es sich lohnen, die Power zu berücksichtigen. Wenn wir eine gute Power haben, dann bedeutet das, dass wir mit hoher Wahrscheinlichkeit einen Effekt entdecken können, wenn es einen gibt. In diesem Fall können wir einen Nullbefund als Evidenz dafür werten, dass ein Effekt einer bestimmten Stärke vermutlich nicht vorliegt.
Studierenden-Perspektive
Was wird von mir erwartet, wenn ich nach der Interpretation von Nullbefunden gefragt werde?
Folgende Punkte sind besonders wichtig:
Absence of evidence is not evidence of absence. Man sollte nicht automatisch von einem Nullbefund auf eine Bestätigung der Nullhypothese zu schließen.
Der Satz aus 1) gilt nicht absolut. Insbesondere sollte man beachten, wie groß die statistische Power ist. Auch ein Blick auf die Konfidenzintervalle zu geschätzten Effekten kann hier sehr informativ sein.
Unter welchen Bedingungen könnten wir denn sagen, dass ein Nullbefund Evidenz gegen das Vorliegen eines Effekts liefert?
Anders gesagt, wann gilt umgekehrt “Absence of evidence is evidence of absence”? Die wichtigste Bedingung dafür ist, dass wir für die kleinste Effektstärke, die uns interessieren würde (die Refenzgröße im Äquivalenztesten) eine ausreichende Power haben.
Was eine ausreichende Power ist, hängt wiederum davon ab, wie wichtig es uns ist, falsch-negative Befunde zu minimieren. Häufig wird als Daumenregel hier eine Power von 80 % angesetzt - doch das würde bedeuten, dass von fünf negativen Befunden einer falsch ist. Wir sollten nicht annehmen, dass es eine magische Schwelle von Power gibt, ab der ein Effekt bei einem Nullbefund als widerlegt gelten kann. Besser ist, zu beobachten, dass die Evidenz gegen den Effekt umso stärker ist, je größer die Power ist. Bei einer Power von 80 % können wir also, als grobe Daumenregel, sagen, dass es sich um erste Evidenz gegen einen Effekt handelt. Bei einer Power von 95 % handelt es sich um starke Evidenz.
In der Psychologie sind Studien mit sehr schwacher Power von 30 % oder weniger leider noch immer sehr häufig. Deshalb bietet der Merksatz Absence of evidence is not evidence of absence tatsächlich eine ganz gute erste Richtlinie (die aber nicht die methodische Beurteilung einer einzelnen Studie ersetzen kann).
Die Bayessche Kritik am Nullhypothesentesten
In diesem Skript haben wir viel über das klassische Nullhypothesentesten geschrieben. Es ist wichtig, das NHST-Denken zu verstehen, um einen Großteil der psychologischen Forschung der vergangenen Jahrzehnte einordnen zu können. Doch unser Horizont sollte nicht auf das NHST-Denken beschränkt bleiben, da es wichtige Kritikpunkte und mächtige Alternativen gibt, allen voran die Bayessche Statistik.
An dieser Stelle können wir leider nicht in die Tiefe dieser Debatte gehen, doch wir möchten das Thema zumindest anreißen.
Ein Kern der bayesschen Kritik lautet: NHST betrachtet nur die Wahrscheinlichkeit der Daten in Anbetracht der Nullhypothese, nicht aber die Wahrscheinlichkeit der untersuchten Hypothesen in Anbetracht der Daten. Letzteres ist aber der eigentliche Faktor, der uns interessiert. Das NHST-Denken kann zu absurden Irrtümern führen, die im XKCD-Comic in Abbildung 3 auf die Schippe genommen werden. Für weitere, tiefergehende Informationen verweisen wir zunächst auf Wagenmakers et al. (2011) und Rouder et al. (2016).

Abbildung 3. XKCD-Comic zur NHST-vs-Bayes Debatte
Literatur
Äquivalenztests: Evidenz für die Nullhypothese im NHST Paradigma
- Lakens, D. (2017). Equivalence Tests: A Practical Primer for t Tests, Correlations, and Meta-Analyses. Social Psychological and Personality Science, 8(4), 355–362. https://doi.org/10.1177/1948550617697177
- Lakens, D., Scheel, A. M., & Isager, P. M. (2018). Equivalence Testing for Psychological Research: A Tutorial. Advances in Methods and Practices in Psychological Science, 1(2), 259–269. https://doi.org/10.1177/2515245918770963
Debatte um Alpha-Niveaus
Benjamin, D. J., Berger, J. O., Johannesson, M., Nosek, B. A., Wagenmakers, E.-J., Berk, R., … Johnson, V. E. (2017). Redefine statistical significance. Nature Human Behaviour, 2(January), 6–10. https://doi.org/10.1038/s41562-017-0189-z
Amrhein, V., & Greenland, S. (2017). Remove, rather than redefine, statistical significance. Nature Human Behaviour, 133(2016), 1. https://doi.org/10.1038/s41562-017-0224-0
Lakens, D., Adolfi, F. G., Albers, C. J., Anvari, F., Apps, M. A. J., Argamon, S. E., … Zwaan, R. A. (2018). Justify your alpha. Nature Human Behaviour, 2(3), 168–171. https://doi.org/10.1038/s41562-018-0311-x
Debatte über NHST vs. Bayes
Rouder, J. N., Morey, R. D., Verhagen, J., Province, J. M., & Wagenmakers, E. J. (2016). Is There a Free Lunch in Inference? Topics in Cognitive Science, 8(3), 520–547. https://doi.org/10.1111/tops.12214
Wagenmakers, E. J., Wetzels, R., Borsboom, D., & van der Maas, H. L. J. (2011). Why Psychologists Must Change the Way They Analyze Their Data: The Case of Psi: Comment on Bem (2011). Journal of Personality and Social Psychology, 100(3), 426–432. https://doi.org/10.1037/a0022790